Schärfentiefe Depth-of-field
Die Schärfentiefe ist ein beliebtes Stilmittel der Photographie. Mit ihrer Hilfe werden die wichtigen Teile des Bildes scharf hervorgehoben und der Rest nur unscharf abgebildet. Die Schärfentiefe bezeichnet die Tiefe des Bildes um die eingestellte Enfernung herum die ausreichend scharf abgebildet wird. Hierbei meint die Tiefe den Abstandsbereich zwischen dem Fernpunk und Nahpunkt des Schärfentiefe Bereichs vom Senor aus gesehen. 'Ausreichend' ist subjektiv und wird üblicherweise über den Zerstreuungskreis definiert. Ein Punkt im Gegenstandsraum dessen Kreis-Abbild auf dem Sensor kleiner ist als der gewählte Zerstreuungskreis wird als scharf definiert. Punkte deren Bilder größere Kreise sind, gelten als unscharf. Obwohl sich dies mathematisch abbilden läßt, ist eine solche Definition von Schärfe subjektiv. The depth-of-field ist a popular stylistic aspect of photography. Exploiting this, the important parts of the image are displayed sharply, while the rest is kept out of focus. The term depth-of-field denotes the depth of the image around the chosen focus distance which is displayed sufficiently sharp. Here depth denotes the distance between the far point and the near point of the sharp region as seen from the sensor. Clearly, 'sufficient' is a subjective criteria and usually it is defined by the circle of confusion. A point in the object space, for which its circle image on the sensor is smaller than the chosen circle of confusion is defined as sharp. Points for which the circle images are larger, are out of focus. Although this can be formulated in mathematical terms, such a definition of sharpness remains subjective.
Bei gegebener Kamera und Objektiv hängt die resultierende Schärfentiefe im wesentlichen von drei, im Rahmen der Grenzen des Systems, frei wählbaren Aufnahmeparametern ab, der eingestellten Entfernung, der Brennweite und der Blendenzahl. Je größer die Entfernung und je kleiner die Brennweite und/oder Blende, um so größer ist die Schärfentiefe. Hierbei entspricht eine kleine Blende einer großen Blendenzahl $k$, und die Blendenzahl bezeichnet das Verhältnis von Brennweite und Öffnungsweite der Linse. Für die exakte Berechnung der Schärfentiefe werden Informationen benötigt die nur dem Objektivhersteller zugänglich sind. Daher sollten Werte die aus Online Rechnern, wie dem auf diesen Seiten bereitgestellten, ermittelt werden, immer nur als Anhaltspunkte gelten und ihre Limitierungen sollten wohl verstanden sein. For a given camera and lens, the resulting depth-of-field mostly depends on three exposure parameters that, within the limits of the system, can be freely chosen, namely the focus distance, the focal length and the f-number. The larger the focus distance and the smaller the focal length and/or aperture, the larger is the depth-of-field. In this a small aperture relates to a large f-number, and the f-number is the ratio of the focal length and the width of the lens opening. For calculating the depth-of-field some information is needed that is only known to the manufacturer of the lens. This means, the values calculated by online calculators, like the one provided here, should only be taken as indications, and their limitations should be well understood.
Im folgenden wird der mathematische Formalismus erklärt und seine Limitierungen diskutiert. Die benutzen Variablen, ihre Definitionen und Einheiten, sowie ein Beispiel sind in der folgenden Tabelle aufgeführt. Dezimalstellen sind durch einen Punkt abgetrennt. Für Leser die nur an der berechneten Schärfentiefe für konkreten Aufnahmeparameter interessiert sind, ist dies ist der direkte Weg zum Schärfentiefe Rechners. In what follows, the formalism is explaind and its limitations discussed. The used variables, their definitions and dimensions as well as an example are given in the following table. The decimal places are separated by a point and there is no comma separator used for indicating thousand. For those who are only interested in the calculated depth-of-field for some concrete exposure parameters, this is the direct path to the Depth-of-field calculator.
| Gruppe Group | Variable Variable | Definition Definition | Einheit Dimension | Beispiel Example |
|---|---|---|---|---|
| Sensor Sensor | $\sx$ | Breite Width | mm | 22.3 mm |
| $\sy$ | Höhe Height | mm | 14.8 mm | |
| $N$ | Linienanzahl Number of lines | 1500 | ||
| Objektiv Lens | $k$ | Blendenzahl F-number $k \in [\kmi, \kma]$ | [5.6, 45] | |
| $f$ | Brennweite Focal length $f \in [\fmi, \fma]$ | mm | [100, 400] mm | |
| $\Emi$ | Naheinstellgrenze Closest focussing distance | cm | 88 cm bei $f=200$ mm 88 cm at $f=200$ mm | |
| $\pup$ | Pupillenmaßstab Pupil scale | unbekannt ($\pup ≡ 1$) unknown ($\pup ≡ 1$) | ||
| $\kp$ | Korrigierte Blendenzahl Corrected f-number $\kp=\frac{k}{\pup}$ | |||
| $d$ | Hauptebenenabstand Distance of principal planes | mm | unbekannt ($d ≡ 0$ mm) unknown ($d ≡ 0$ mm) | |
| Aufnahme Exposure | $f$ | Brennweite Focal length | mm | 400 mm |
| $k$ | Blendenzahl F-number | 8 | ||
| $E$ | Fokus Entfernung Focus distance | cm | 200 cm | |
| $\beta$ | Abbildungsmaßstab Aspect ratio | |||
| Berechnung Calculation | z | Zerstreuungskreis Circle of confusion | cm | 0.0018 cm |
| $B$ | Bildgröße Image size | cm | ||
| $G$ | Gegenstandsgröße Object size | cm | ||
| $b$ | Bildweite Image distance | cm | ||
| $g$ | Gegenstandsweite Object distance | cm | ||
| $\gn$ | Gegenstandsweite Nahpunkt Near point object distance | cm | ||
| $\gf$ | Gegenstandsweite Fernpunkt Far point object distance | cm | ||
| $\gh$ | Hyperfokale Gegenstandsweite Hyperfocal object distance | cm | ||
| $\bh$ | Hyperfokale Bildweite Hyperfocal image distance | cm | ||
| $\En$ | Fokus Entfernung Nahpunkt Near point focus distance | cm | 199.8 cm | |
| $\Ef$ | Fokus Entfernung Fernpunkt Far point focus distance | cm | 200.1 cm | |
| $\Eh$ | Hyperfokale Fokus Entfernung Hyperfocal focus distance | cm | 112129 cm = 112.1 m | |
| $T$ | Schärfentiefe Depth-of-field | cm | 0.27 cm |
Die folgende Skizze zeigt das Bild $B$ eines Gegenstands $G$, dass durch ein Objektiv erzeugt wird. Die optische Abbildung durch das Objektiv wird hierbei durch die Abbildung einer dicken Linse beschrieben. Das Objektiv ist rotations-symmetrisch um die optische Achse OA. Zusätzlich ist die Bedeutung der in den folgenden Rechnungen benutzten Variablen gezeigt. The below sketch shows the image $B$ of an object $G$, created by a camera lens. In this, the image of the camera lens is described as the one produced by one thick lens. The camera lens is rotational symmetric around the optical axis OA. In addition, the meaning of the variables used in the following calculations is indicated.
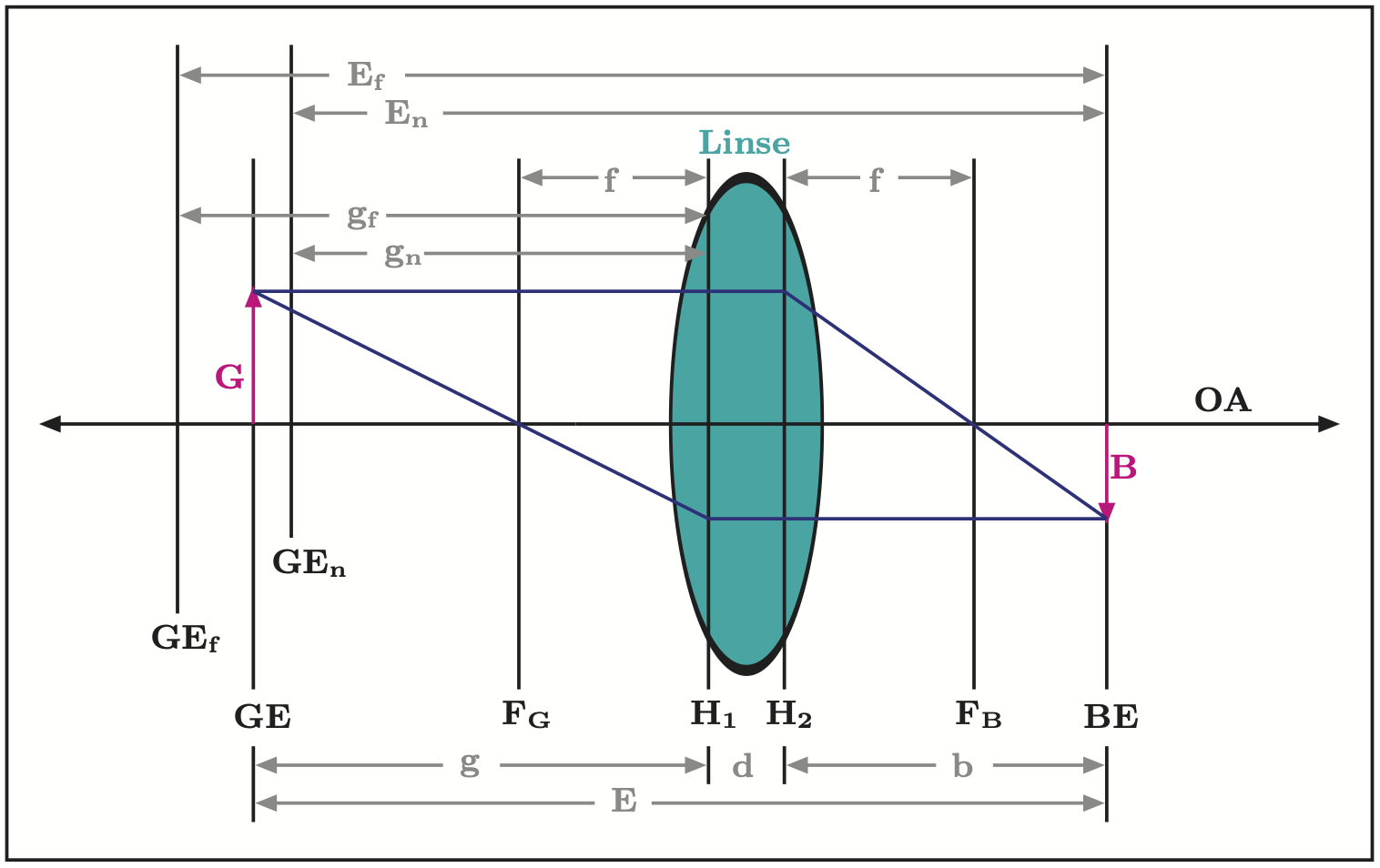
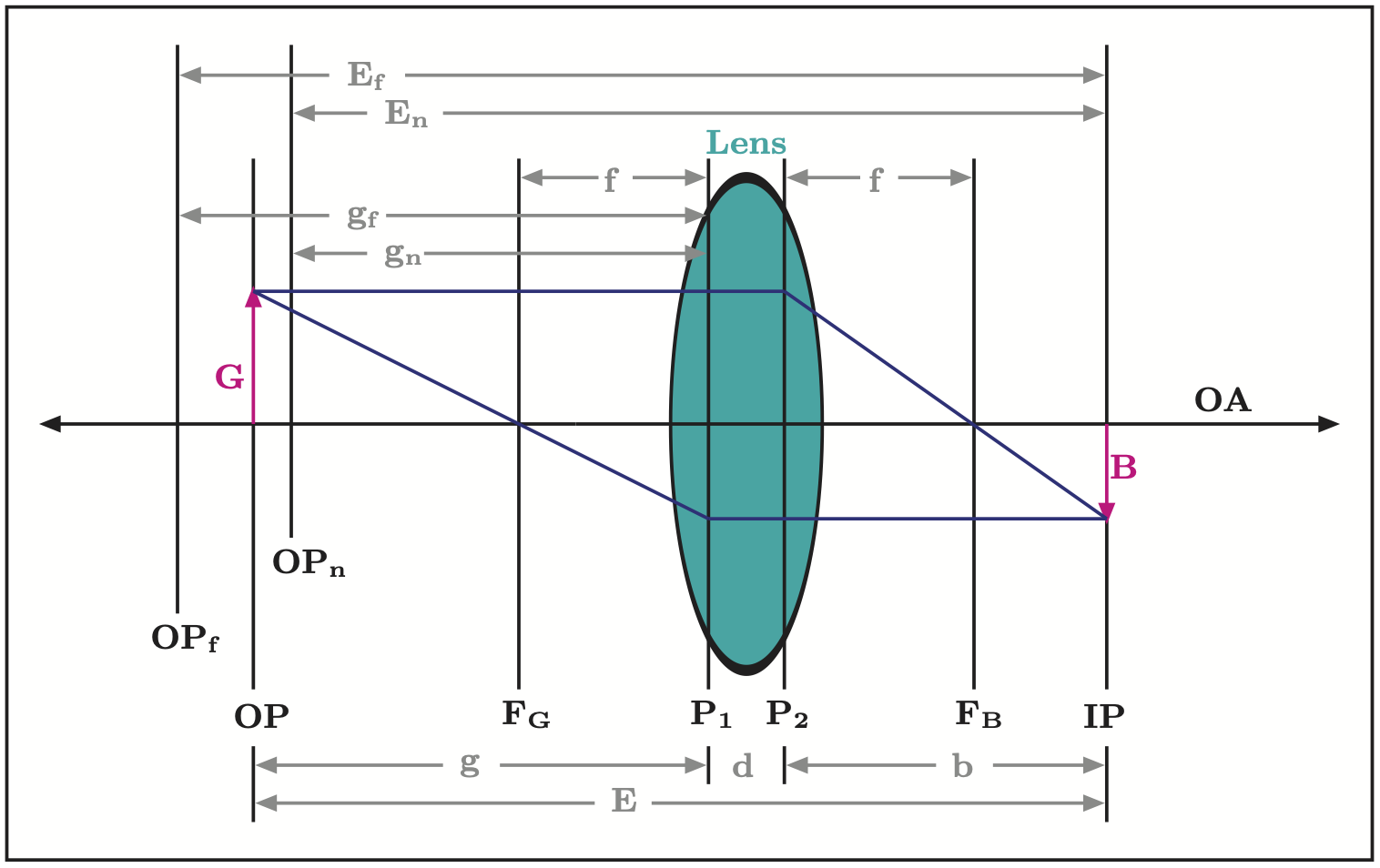
Der Zerstreuungskreis $z$, Gleichung Gl.\ref{Eq:circ}, ist so definiert, daß das menschliche Auge zwei Punkte eines Bildes mit diesem Abstand aus einer festen, aber willkürlich angenommenen Beobachtungsentfernung gerade noch auflösen kann. Berechnet wird $z$ aus dem Verhältnis der Diagonale des Sensors und einer aus obigen Überlegungen abgeleiteten festen Zahl $N$, üblicherweise $N=1500$. Soll ein Photo stark vergrößert werden, sind die Anforderungen höher und $N$ wird entsprechend größer gewählt. The circle of confusion, equation Eq.\ref{Eq:circ}, is defined such that the human eye can barely separate two points within an image that have a distance corresponding to the diameter of the cicle of confusion, when observed from a defined, but arbitrary observing distance. The value of $z$ is calculated from the diagonal of the sensor and a fixed number $N$ derived from the above considerations, typically using $N=1500$. In case an image should be enlarged, the requirement are stronger and a larger $N$ is chosen.
\begin{equation}\label{Eq:circ} \tag{1} z = \frac{\sqrt{\sx^2 + \sy^2}}{N} \end{equation}Für eine dünne Linse mit der Brennweite $f$ gilt die Linsengleichung Gl.\ref{Eq:lens}. Hierbei bezeichnen $g$ die Gegenstandsweite, also den Abstand der Gegenstandsebene GE von der Linse im Gegenstandsraum, und $b$ die Bildweite also den Abstand der Bildebene BE von der Linse im Bildraum. Beide Größen sind so gewählt, dass sie nur positive Werte annehmen können $b,g>0.$ Bei gleichem Medium (hier Luft) im Gegenstands- und Bildraum, befinden sich die Brennweiten Ebenen $F_G$ und $F_B$ im gleichen Abstand von der Linse (oder von der jeweiligen Hauptebene, siehe unten). Die eingestellte Entfernung $E$ ist dann die Summe der Gegenstands- und Bildweite, $E=g+b$. Durch Umstellen der Gleichung lässt sich jeweils einer der beiden Parameter $g$ oder $b$ durch den jeweils anderen und die Brennweite ausdrücken. In allen Gleichungen auf dieser Seite ist das Produkt zweier Größen ohne Rechenzeichen geschrieben, also $fb ≡ f\cdot b$. For a thin lens with focal length $f$ the lens equation Eq.\ref{Eq:lens} applies. In this $g$ is the object distance, which means the distance of the object plane OP to the lens in object space and $b$ the image distance, i.e. the distance of the image plane $IP$ from the lens in image space. Both quantities are chosen such that they can only have positive values, $b,g>0.$ An identical medium (here air) in object space and image space, results in identical distances of the focal-length planes $F_G$ and $F_B$ from the lens plane (or the respective principal planes, see below). The chosen focal distance $E$ is the sum of the object- and image distance, $E=g+b$. Be re-arranging the equation, one can express each one of those quantities by the respective other quantity and the focal length. In all equations shown on this page, the product of two quantities is written without an arithmetic operator, i.e. $fb ≡ f\cdot b$.
\begin{equation}\label{Eq:lens} \tag{2} \frac{1}{f} = \frac{1}{b} + \frac{1}{g},\quad g = \frac{f b}{b-f}, \quad b = \frac{f g}{g-f} \end{equation}Der Abbildungsmaßstab $\beta$, Gl.\ref{Eq:aspect} ist das Verhältnis von Bildgröße $B$ zu Gegenstandsgröße $G$. Mit Hilfe von Strahlensätzen lässt sich ein Zusammenhang von $\beta$ und $g$ ermitteln. The aspect ratio $\beta$, Eq.\ref{Eq:aspect} is the ratio of the image size $B$ and the object size $G$. With the help of the theorems of intersecting lines one can derive a relation of $\beta$ und $g$.
\begin{equation}\label{Eq:aspect} \tag{3} \beta = \frac{B}{G} = \frac{b}{g} = \frac{f}{g-f},\quad g = f\,(1+\frac{1}{\beta}) \end{equation}Objektive bestehen aus vielen Linsen die in mehreren Gruppen angeordnet sind. Zum Beispiel enthält das von mir genutzte Canon RF100 Objektiv 17 Linsen in 9 Gruppen. Für eine solche Anordnung kann das Modell einer dünnen Linse nicht mehr genutzt werden. Es zeigt sich jedoch, daß solche Linsensysteme als eine dicke Linse mit zwei Hauptebenen H$_1$ und H$_2$ mit Abstand $d$ beschrieben werden können. Bei der Konstruktion der Strahlenoptik werden die vom Gegenstand ausgehenden Strahlen an der zweiten Hauptebene, und die vom Bild ausgehenden, an der ersten Hauptebene gebrochen. Nun bezeichnet $g$ den Abstand von der ersten Hauptebene im Gegenstandsraum und $b$ den Abstand von der zweiten Hauptebene im Bildraum. Da die Hauptebenen nur Hilfsebenen bei der Berechnung der Abbildung sind, kann $d$ auch negativ sein, was bedeutet, dass die erste Hauptebene weiter vom Objekt entfernt ist als die Zweite. Dies ist auch häufig der Fall, da es den Bau eines kompakten Objektiv ermöglicht. Die obigen Gleichungen gelten auch für ein solches System. Allerdings ist nun in der eingestellten Entfernung der Abstand $d$ zu berücksichtigen, Gl.\ref{Eq:focdis}. Wegen der unabhängigen Bewegung der Linsengruppen wird $d$ im allgemeinen eine Funktion der eingestellten Entfernung $E$ sein. Im letzten Schritt wurde noch $b$ mit Hilfe der Gl.\ref{Eq:lens} ersetzt. Camera lenses consist of many individual lenses arranged in several groups. For example, the Canon RF100 camera lens which I use contains 17 lenses in 9 groups. For such a system, the model of a single thin lens is not applicable. However, it can be shown that such systems can be described by one thick lens with two principal planes P$_1$ und P$_2$ located at a distance $d$. When constructing the ray optics, the rays originating from the object will be reflected at the second principle plane, while the ones originating from the image will be reflected at the first principle plane. In this situation, $g$ is the distance calculated from the first principle plane in object space and $b$ is the distance calculated from the second principle plane in image space. Since the principal planes are work planes for calculating the image of the object, $d$ can be negative, which means that the first principle plane is further away from the object than the second. In practise this is often the case, because it allows for designing compact camera lenses. The above equations are also valid for such a system. However, the distance $d$ has to be included in the calculation of $E$, Eq.\ref{Eq:focdis}. Because of independent movements of groups of lenses, $d$ will in general not be constant, but a function of $E$. In the last step $b$ was replaced with the help of Eq.\ref{Eq:lens}.
\begin{equation}\label{Eq:focdis} \tag{4} E = g + d + b = g + d + \frac{f g}{g-f} \end{equation}Zur alternativen Berechnung der Schärfentiefe als Funktion eines gewünschten Abbildungsmaßstabs $\beta$, wird in der Gl.\ref{Eq:focdis} die Variable $g$ mit Hilfe der Gl.\ref{Eq:aspect} durch $\beta$ ersetzt. To instead calculate the depth-of-field as a function of a wanted aspect ratio $\beta$, the variable $g$ in Eq.\ref{Eq:focdis} is replaced by $\beta$ with the help of Eq.\ref{Eq:aspect}.
\begin{equation}\label{Eq:focdisbeta} \tag{5} E = d + 2f + f(\frac{1}{\beta}+\beta) \end{equation}Unabhängig von der genutzten Eingangsvariablen ist sicherzustellen, dass fü das jeweilige Objektivs weder die Naheinstellgrenze unterschritten, noch der maximale Abbildungsmaßstabs überschritten wird. Die folgende Rechnung ist identisch unabhängig davon wie $E$ ermittelt wurde. Independent of the used input variable, it has to be ensured that for the given camera lens neither the closest focusing distance is nor the largest aspect ratio is exceeded. The following calculation proceeds identical, irrespectively of how $E$ was derived.
Da der Hauptebenenabstand dem Schärfentiefe-Rechner nicht zugänglich ist, wird $d ≡0$ genutzt, wodurch sich ein kompakter Zusammenhang $E$ als Funktion von $g$ ergibt. Wenn zusätzlich die Gegenstandsweite wesentlich größer ist als die Brennweite, $g \gg f$, fallen die Entfernungeinstellung un die Gegenstandsweite zusammen. Je ähnlicher also $g$ und $d$ sind, umso approximativer ist das Resultat. Die Situation von typischen Makroaufnahmen wird daher schlecht beschrieben, während bei Entfernungeinstellung von einigen zig Metern die Werte von $d$ und auch von $f$ nur eine untergeordnete Rolle spielen. Im Schärfentiefe-Rechner dieser Seite wird, da nicht bekannt, $d$ notgedrungen vernachlässigt, aber die bekannten Abhängigkeiten von $f$ vollumfänglich genutzt. Since the distance of the principal planes is not known to the depth-of-field calculator, $d ≡0$ is used, which results in a compact formula for $E$ as a function of $g$. When in addition the object distance is much larger that the focal length $g \gg f$, the object distance and the focus distance coincide. The closer $g$ and $d$, the more approximative is the result. Consequently, the situation present in typical macro images is described poorly, while for settings for which the focus distance is several tenth of meters, the values of $d$ and also of $f$ are of minor importance. In the depth-of-field calculator on this page, unavoidably $d$ is ignored, while all known dependencies on $f$ are fully kept.
\begin{equation}\label{Eq:focdisdn} \tag{6} d ≡0 \Rightarrow E = g + \frac{f g}{g-f} = g\,(1+\frac{f}{g-f}) \approx g\,(1+\frac{f}{g}) = g + f \approx g \end{equation}Jedes Objektiv hat eine Austritspupille und eine Eintrittspupille, die die Strahlenbündel die durch das Objektiv gelangen können begrenzen. Das Verhältnis der beiden wird als Pupillenmaßstab $\pup$ bezeichnet. Durch den Pupillenmaßstab kann die eingestellte Blende $k$ eventuell nicht voll wirksam sein. In dem Fall ist die korrigierte Blendezahl $\kp=\frac{k}{\pup}$ in den Formeln der Schärfentiefe einzusetzen. Da der Pupillenmaßstab auch nicht bekannt ist, wird üblicherweise mit $k$ gerechnet, also $\pup ≡ 1$ angenommen. Wegen ihre geringen Schärfentiefe lassen sich mit Objektive mit großen Blendenöffnungen (kleinen Blendenzahlen) Objekte gut vor unscharfen Hintergrund freistellen Daher sind sie sehr pupulär und teuer. Es ist daher unwahrscheinlich, dass in diesen Objektiven Pupillenmaßstäbe vorhanden sind, welche die effektive Blende einschränkten. Für große Blendenzahlen ist die Lamellenblende einschränkender als die Objektiv Pupillen. Every camera lens has an exit pupil and an entrance pupil, which effectively restrict the cones of rays that can pass the lens. The ratio of the two is known as pupil scale. For a given pupil scale the selected aperture $k$ may not be fully active. In this case an corrected f-number $\kp=\frac{k}{\pup}$ has to be used in the formulas for the depth-of-field. Since the pupil scale is also not known, normally $k$ is used, i.e. $\pup ≡ 1$ is assumed. Because of the small depth-of-field, large aperture (small f-numbers) lenses allow for well isolating the object in front of a blurred background. For this reason they are very popular and expensive. It is thus not likely that in these lenses small pupil scales are present, which would reduce the effective aperture. For large f-numbers, the iris is more restrictive than the lens pupils.
Die üblicherweise angegebenen Blendenzahlen, zum Beispiel F5.6, sind gerundet. Die Formel für ganze Blendenzahlen ist $k=(\sqrt{2})^{(n-1)}$ mit $n=1,2,3\ldots$ als index. Die Formeln für halbe und drittel Blendenzahlen sind ähnlich. Für $n=6$ ergibt sich $k=(\sqrt{2})^5=5.657$, also eine Abweichung von 5.6 von etwa einem Prozent, was die übliche Größe dieser Abweichungen ist. The typically used f-numbers, like F5.6, are rounded numbers. The formula for integral f-numbers is $k=(\sqrt{2})^{(n-1)}$ with $n=1,2,3\ldots$ as index. The formulas for half or one third f-numbers are similar. For $n=6$ this results in $k=(\sqrt{2})^5=5.657$, which means a deviation from 5.6 of about one per cent, which is the typical size of these deviations.
Da die Blende immer nur als Produkt mit dem, durch Annahme von $N$, frei gewählten $N$ Zerstreuungskreis auftritt, also als $kz$, sind beide Effekte nicht so erheblich, da $z$ sowieso eine subjektive Definition ist. Mein Schärfentiefe-Rechnern benutzt die vom Nutzer eingegebene Blendenzahl unkorrigiert, wenn gewüncht kann also 5.657 genutzt werden. In jedem Fall kann der Einfluss durch Variation von $N$ abgeschätzt werden. Because in all formulas the aperture appears only as a product with the, due to the choice of $N$, freely chosen circle of confusion, namely $kz$, both effects are not so important. My depth-of-field calculater uses the number provided by the user without any correction, so if wanted 5.657 can be used. In any case, the impact can be estimated by varying $N$.
Da die Gegenstandsweite nicht bekannt ist, muss sie aus der Entfernungseinstellung berechnet werden. Nach Umstellen von Gl.\ref{Eq:focdis} und dem Ersetzen von $b$ aus der Linsengleichung, Gl.\ref{Eq:lens}, ergibt sich in quadratische Gleichung für $g$. Deren Lösung ist Gl.\ref{Eq:gofE}. Given the object distance is unknown, it has to be derived from the focus distance. Re-arranging Eq.\ref{Eq:focdis} and replacing $b$ by using the lens equation, Gl.\ref{Eq:lens}, a quadratic form for $g$ is derived. The solution of this is:
\begin{equation}\label{Eq:gofE} \tag{7} g = \frac{E-d}{2} + \sqrt{\left(\frac{E-d}{2}\right)^2 - f (E-d)} = \frac{E-d}{2} \left[1 + \sqrt{1 - \frac{4f}{E-d}}\,\right] \end{equation}Das der Hauptebenenabstand bei realen Objektiven sehr wohl eine Rolle spielt, lässt sich an folgendem Beispiel sehen. Der Term unter der Wurzel in Gl.\ref{Eq:gofE} muss mindestens Null sein, damit ergibt sich eine minimale Entfernung, die sogenannte Naheinstellgrenze von $E \ge 4f + d$. Für $d=0$ muß die eingestellte Enfernung damit mindestens vier mal die Brennweite betragen. Für das RF 100 Objektiv, bedeutete dies $E\ge 40$ cm. Die echte Naheinstellgrenze dieses Objektivs beträgt aber nur 26 cm, damit verschwindet die Wurzel für $d=-140$ mm also $d=-1.4f$. Offensichtlich sind Schärfentiefe-Rechner die auf $d=0$ basieren für diesen Fall nicht nutzbar. The fact that for real camera lenses the distance of the principal planes is important, can be seen from the following example. The term under the square-root in Eq.\ref{Eq:gofE} needs to be at least zero, which results in a minimum distance, the so-called closest focussing distance $E \ge 4f + d$. For $d=0$ the focus distance has to be at least for times the focal length. For the RF 100 lens, this means $E\ge 40$ cm. The near focus limit of this camera lens is just 26 cm, which means the square root vanishes for $d=-140$ mm this is $d=-1.4f$. Clearly, in this case depth-of-field calculators using $d=0$ are not applicable.
Nun lässt sich für gegebene Werte ($E, k, f$) die Fernpunkt Gegenstandsweite $\gf$, Gl.\ref{Eq:gfar}, und die Nahpunkt Gegenstandsweite $\gn$, Gl.\ref{Eq:gnear}, des Schärfentiefebereichs berechnen. Die jeweiligen Gegenstandsebenen sind GE$_f$ und GE$_g$. Die Schärfentiefe $T$, Gl.\ref{Eq:depthoffield}, ist dann die Differenz aus diesen beiden Werten. Now, for given values of ($E, k, f$), the far point object distance $\gf$, Gl.\ref{Eq:gfar}, and the near point object distance $\gn$, Gl.\ref{Eq:gnear}, of the depth-of-field, can be calculated. The respective object planes are OP$_f$ und OP$_g$. The depth-of-field $T$, Gl.\ref{Eq:depthoffield}, is the difference of these two values.
\begin{equation}\label{Eq:gfar} \tag{8} \gf = \frac{f^2 g}{f^2 - k z\,(g-f)} \end{equation} \begin{equation}\label{Eq:gnear} \tag{9} \gn = \frac{f^2 g}{f^2 + k z\,(g-f)} \end{equation} \begin{equation}\label{Eq:depthoffield} \tag{10} T = \gf - \gn = 2kz \frac{f^2g\,(g-f)}{f^4 - k^2 z^2f^2\,(g-f)^2} \end{equation}Eine wichtige Kenngröße eines Kamera+Objektiv Systems ist die hyperfokale Gegenstandsweite $\gh$ Gl.\ref{Eq:ghyp}, da bei dieser Gegenstandsweite der Schärfentiefebereich am größten ist. Die hyperfokale Gegenstandsweite ergibt sich wenn der Nenner in Gl.\ref{Eq:gfar} gleich Null ist und damit der Bruch unendlich, $\gf = ∞$, also bei $f^2 = k z\,(\gh-f)$. Einsetzen in Gl.\ref{Eq:gnear} ergibt $\gn=\frac{\gh}{2}$. Der scharfe Bereich ist also von der halben hyperfokalen Gegenstandsweite bis nach unendlich, $[\frac{\gh}{2}, ∞]$. An important parameter of a camera+lens system is the hyperfocal object distance $\gh$ Gl.\ref{Eq:ghyp}, since for this object distance the depth-of-field is largest. The hyperfocal object distance is obtained when the denominator in Gl.\ref{Eq:gfar} vanishes, such that the ratio evaluates to $\gf = ∞$, i.e. at $f^2 = k z\,(\gh-f)$. Inserting this into Eq.\ref{Eq:gnear} the value of $\gn=\frac{\gh}{2}$ is obtained. The sharp region thus extend from half the hyperfocal object distance up to infinity, $[\frac{\gh}{2}, ∞]$.
\begin{equation}\label{Eq:ghyp} \tag{11} \gh = f\,(1+\frac{f}{k z}), \quad\quad kz = \frac{f^2}{\gh-f} \end{equation}Für $g>0$, ist die Funktion für $\gf$, Eq.\ref{Eq:gnear}, eine Hyperbel mit zwei Ästen, von denen nur der Ast $g\le\gh$ eine physikalische Lösung ist. Für größere Werte von $g$ wird diese Funktion negativ. Daher ist für $g>\gh$, die Fernpunkt Gegenstandweite immer bei $\gf = ∞$. For $g>0$, the function for $\gn$, Eq.\ref{Eq:gnear}, is a hyperbola with two branches, of which only the branch $g\le\gh$ is a physical solution. For larger values of $g$, the function turns negative. Thus, for $g>\gh$, the far point object distance is always at $\gf = ∞$.
An der Kamera einstellen kann man aber nur die hyperfokale Entfernung $\Eh$. Mit der Gl.\ref{Eq:focdis} für $E$ ergibt sich die Gl.\ref{Eq:ehyp} für $\Eh$. Üblicherweise werden hierbei zwei Näherungen gemacht: 1) $d=0$ (oder $d \ll \gh+\bh$) und 2) $f \ll \gh$. Dies ist meistens erfüllt, wie auch im Beispiel in der obigen Tabelle. So wird üblicherweise nicht zwischen $\gh$ und $\Eh$ unterschieden wenn die über die Hyperfokale Entfernung gesprochen wird. The camera only allows for chosing the hyperfocal focus distance $\Eh$. Using Eq.\ref{Eq:focdis} for $E$ the Eq.\ref{Eq:ehyp} is obtained for $\Eh$. Typically, two approximations are made here: 1) $d=0$ (or $d \ll \gh+\bh$) and 2) $f \ll \gh$. These conditions are often fulfilled, as also for the example in the above table. As a result, frequently the terms $\gh$ und $\Eh$ are not distinguished when talking about the hyperfocal distance.
\begin{equation}\label{Eq:ehyp} \tag{12} \Eh = \gh + d + \bh \approx \gh + \frac{f \gh}{\gh-f} = \gh\,(1+\frac{f}{\gh-f}) \approx \gh + f \approx \gh \end{equation}Bei einigen Schärfentiefe-Rechnern findet man die folgenden Formeln für $\gf$, Gl.\ref{Eq:gfarhyp}, und $\gn$, Gl.\ref{Eq:gnearhyp}, beide ausgedrückt als Funktion der hyperfokalen Gegenstandsweite $\gh$. Diese Formeln erhält man aus Gl.\ref{Eq:gfar} und Gl.\ref{Eq:gnear} durch Ersetzen von $kz$ durch den eqivalenten Ausdruck als Funktion von $\gh$ aus der Gl.\ref{Eq:ghyp}. Diese Formeln sind damit equivalent. Sie enthalten aber nur Gegenstandsweiten und keine Entfernungseinstellungen. Die Schärfentiefe $T$, Gl.\ref{Eq:depthoffieldhyp}, ist die Differenz aus diesen beiden Werten. In some depth-of-field calculators one finds the following formulas for $\gf$, Eq.\ref{Eq:gfarhyp}, and $\gn$, Eq.\ref{Eq:gnearhyp}, both expressed as functions of the hyperfocal object distance $\gh$. They are obtained from Eqs.\ref{Eq:gfar} and Eq.\ref{Eq:gnear} by replacing $kz$ by the equivalent expression from Eq.\ref{Eq:ghyp} as a function of $\gh$. These formulas are thus equivalent. However, they only contain object distances and no focus distances. The depth-of-field $T$, Gl.\ref{Eq:depthoffieldhyp}, is the difference of these two values.
\begin{equation}\label{Eq:gfarhyp} \tag{13} \gf = \frac{g\,(\gh -f)}{\gh - g} \end{equation} \begin{equation}\label{Eq:gnearhyp} \tag{43} \gn = \frac{g\,(\gh -f)}{\gh + g - 2 f} \end{equation} \begin{equation}\label{Eq:depthoffieldhyp} \tag{15} T = \gf - \gn = \frac{2g(\gh-f)(g-f)}{(\gh-g)(\gh+g-2f)} \end{equation}Wenn, anstatt von $g$, die vom Nutzer angegebene Fokus Entfernung $E$ in diese Formel eingesetzt wird, bedeutet dies die Annahme $E=g$, also die Vernachlässigung von $d$ und $b$, also $b=d=0$ in Gl.\ref{Eq:focdis}. Der numerische Effekt ist oft signifikant, da einige Funktionen sehr steil sind, insbesondere $\gf$ in der Nähe von $\gh$. If, instead of $g$ the user supplied focus distance $E$ is inserted into this formuala, this means the assumption $E=g$ is made. In this case $d$ and $b$ are ignored in Eq.\ref{Eq:focdis} and thus $b=d=0$ is used. Often, the numerical impact is significant, since some functions are very steep, especially $\gf$ close to $\gh$.
Zur Berechnung der Entfernung des Fernpunkts $\Ef$ und Nahpunkts $\En$ werden $\gf$ und $\gn$ in Gl.\ref{Eq:focdisdn} für $d ≡0$ eingesetzt. Da nicht neu fokussiert wird, bleibt die Bildweite $b$, hier ausgedrückt als Funktion von $g$ und $f$, gleich. Da dieser Term in $\Ef$ und $\En$ enthalten ist, verschwindet er in der Differenz, und die Schärfentiefe bleibt unverändert, wie es sein muß. For calculating the distances of the far point $\Ef$ and near point $\En$, $\gf$ und $\gn$ are inserted into Eq.\ref{Eq:focdisdn} for $d ≡0$. Since the focus distance is fixed, the image distance $b$, here expressed as a function of $g$ and $f$, stays the same. Given this term is identical for $\Ef$ and $\En$, it vanishes in their diference and the depth-of-field is unchanged as it should.
\begin{equation}\label{Eq:Efar} \tag{16} \Ef = \gf + b = \gf + \frac{fg}{g-f} = = \frac{f^2 g}{f^2 - k z\,(g-f)} + \frac{fg}{g-f} = \frac{g\,(\gh -f)}{\gh - g} + \frac{fg}{g-f} \end{equation} \begin{equation}\label{Eq:Enear} \tag{17} \En = \gn + b = \gn + \frac{fg}{g-f} = \frac{f^2 g}{f^2 + k z\,(g-f)} + \frac{fg}{g-f} = \frac{g\,(\gh -f)}{\gh + g - 2 f} + \frac{fg}{g-f} \end{equation}Der Bereich der Schärfentiefe ist nicht symmetrisch um die Fokus Ebene in der eingestellten Entfernung vom Sensor. Der Teil des Bereichs von der Kamera weg wird mit $\df$ bezeichnet, der Teil zur Kamera hin, mit $\dn$. Zur Verdeutlichung des Sachverhalts, wird die Differenz für hier $\dn$ so geählt, dass $\dn \lt 0$. The range of the depth-of field is not symmetric around the focus plane at the chosen focus distance from the sensor. The part of this range away from the camera is denoted by $\df$, the one towards the camera by $\dn$. To make this situation more clear, here the difference for $\dn$ is chosen such that $\dn \lt 0$.
\begin{equation}\label{Eq:dfar} \tag{18} \df = \Ef - E \gt 0 \end{equation} \begin{equation}\label{Eq:dnear} \tag{19} \dn = \Ef - E \lt 0 \end{equation}Die oben angegebenen Formels sind die Basis meines Schärfentiefe Rechners. The above listed formulas are the basis for my Depth-of-field calculator.